The other day, after working on a few Sudokus and really getting the hang of them :-), I thought to apply a little combinatoric; i.e., how many variations of the same Sudoku are possible?
Well, you can easily swap complete rows or columns — within each of the respective 3x blocks to leave their integrity intact — and you can swap the complete column or row with the 3x blocks.
E.g., you can swap row 2 with row 1 or row 3, or column 7 with column 8 or column 9; or you can swap the rows 4 – 6 with rows 1 – 3 or rows 7 – 9, or columns 7 – 9 with columns 1 – 3 or columns 4 – 6.
So… swapping the rows within the 3x boundaries, and there are three of those; then the three row blocks themselves; ditto for the columns and column blocks:
(3!)³ • (3!) • (3!)³ • (3!)
or
1’679’616 combinations
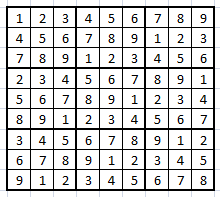
Here my basic Sudoku I developed „on the fly“:
[jm’s Sudoku]
But then, the show won’t stop here! 🙂
Consider you can also swap the numbers; e.g., exchange 1 with 7 and/or 3 with 9, and what so on, resulting to
9!
or
additional 363’880 combinations
Leaves me with the one question: is my Sudoko shown — under consideration of the various combinations listed — the only one?
© August 2009 Jürgen Menge, San José